CSC413 Neural Networks and Deep Learning
Lecture 8
Lecture Overview
Last Week
- CNN Feature Visualization and Interpretation
- Transfer Learning
- Adversarial Examples
- Influence Functions
This week
- Recurrent Neural Networks
- Sentiment Analysis with Recurrent Neural Networks
- Gradient Explosion and Vanishing
- Text Generation with RNN
- Sequence-to-Sequence Modelling
Recurrent Neural Networks
Goal and Overview
Sometimes we’re interested in making predictions about data in the form of sequences. Some examples are:
- Given the price of a stock in the last week, predict whether stock price will go up
- Given a sentence (sequence of chars/words) predict its sentiment
- Given a sentence in English, translate it to French
This last example is a sequence-to-sequence prediction task, because both inputs and outputs are sequences.
Language Model
We have already seen neural language models that make the Markov Assumption:
\[p(w_i | w_1, \ldots, w_{i-1}) = p(w_i | w_{i-3}, w_{i-2}, w_{i-1})\]
This means the model is memoryless, so it can only use information from its immediate context.
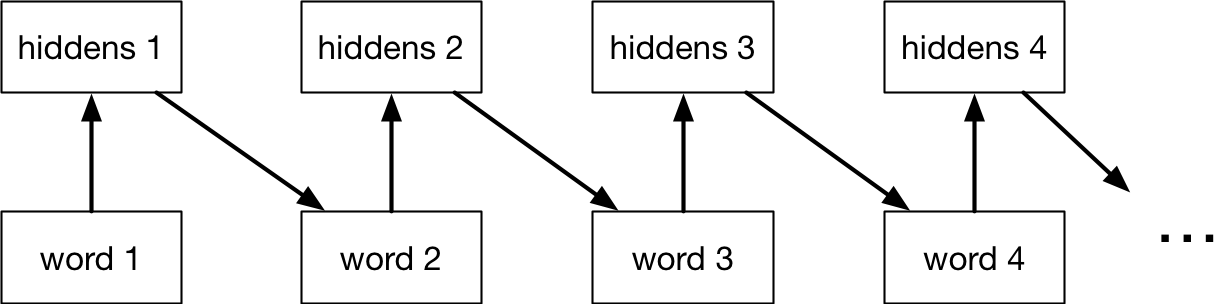
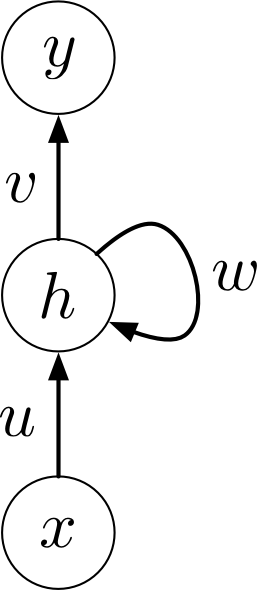
Recurrent Neural Network
But sometimes long-distance context can be important.
If we add connections between the hidden units, it becomes a recurrent neural network (RNN).
Having a memory lets an RNN use longer-term dependencies:
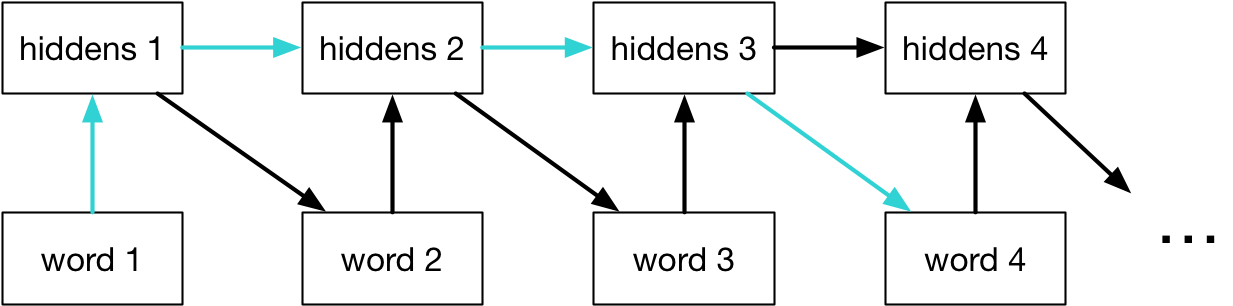
RNN Diagram
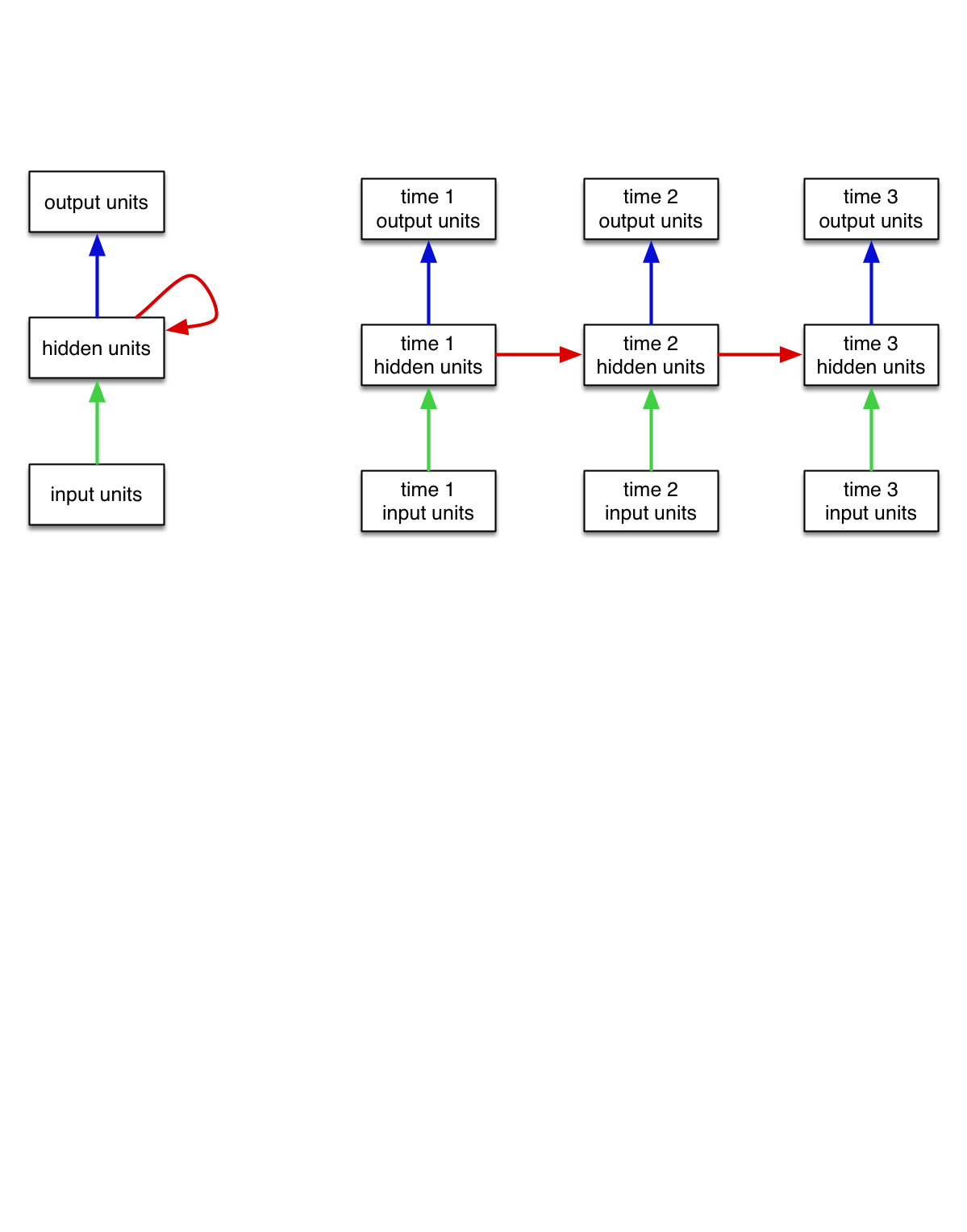
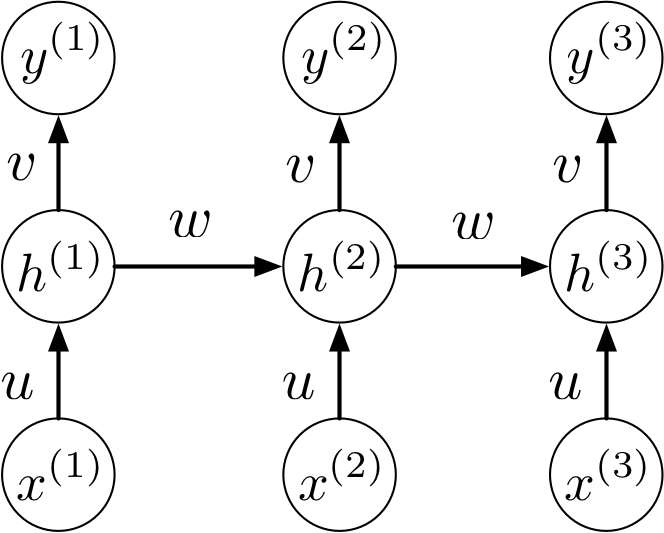
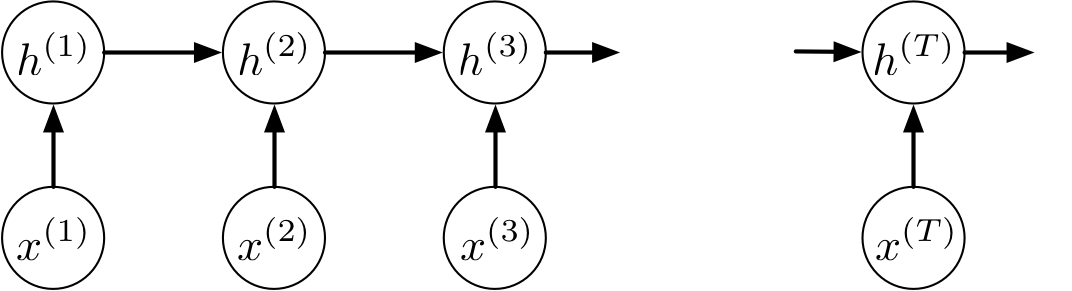
We can think of an RNN as a dynamical system with one set of hidden units which feed into themselves. The network’s graph would then have self-loops.
We can unroll the RNN’s graph by explicitly representing the units at all time steps. The weights and biases are shared between all time steps
Simple RNNs
Let’s go through a few examples of very simple RNNs to understand how RNNs compute predictions.
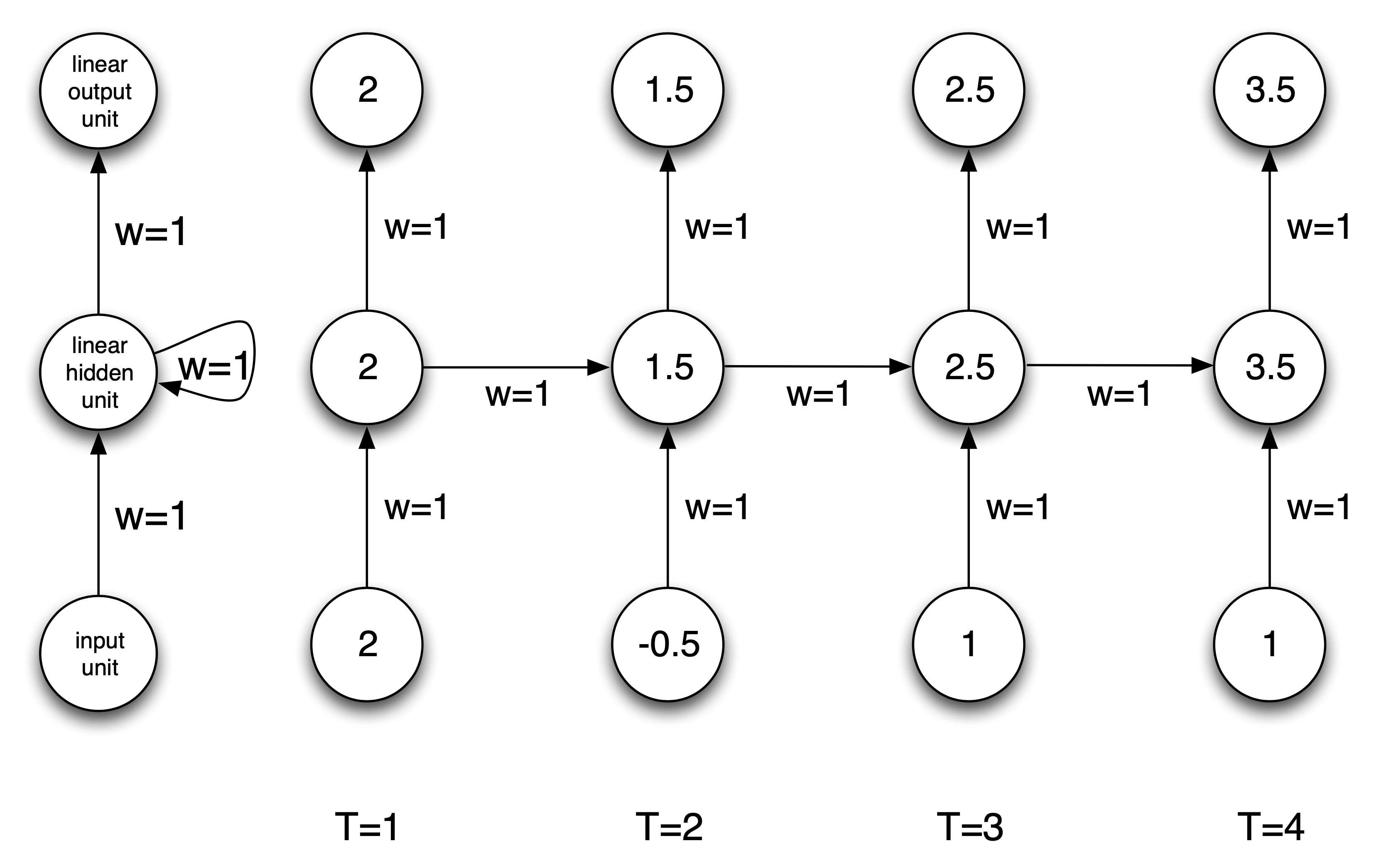
Simple RNN Example: Sum
This simple RNN takes a sequence of numbers as input (scalars), and sums its inputs.
Simple RNN Example 2: Comparison
This RNN takes a sequence of pairs of numbers as input, and determines if the total values of the first or second input are larger:
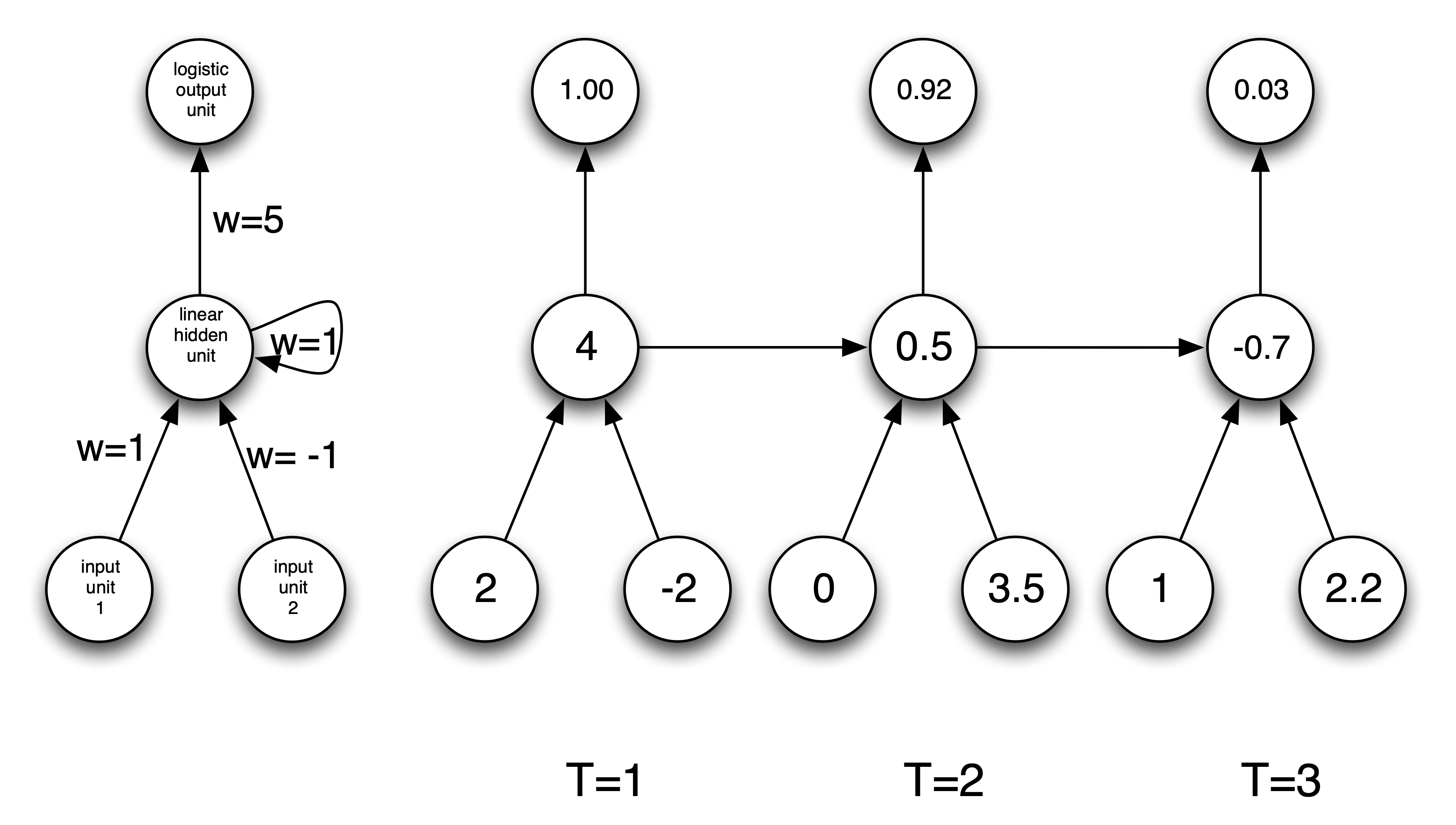
Simple RNN Example 3: Parity
Assume we have a sequence of binary inputs. We’ll consider how to determine the parity, i.e. whether the number of 1’s is even or odd. We can compute parity incrementally by keeping track of the parity of the input so far:
| Parity bits: | Input: | |
|---|---|---|
| 0 1 1 0 1 1 | \(\longrightarrow\) | 0 1 0 1 1 0 1 0 1 1 |
Each parity bit is the XOR of the input and the previous parity bit. Parity is a classic example of a problem that’s hard to solve with a shallow feed-forward net, but easy to solve with an RNN.
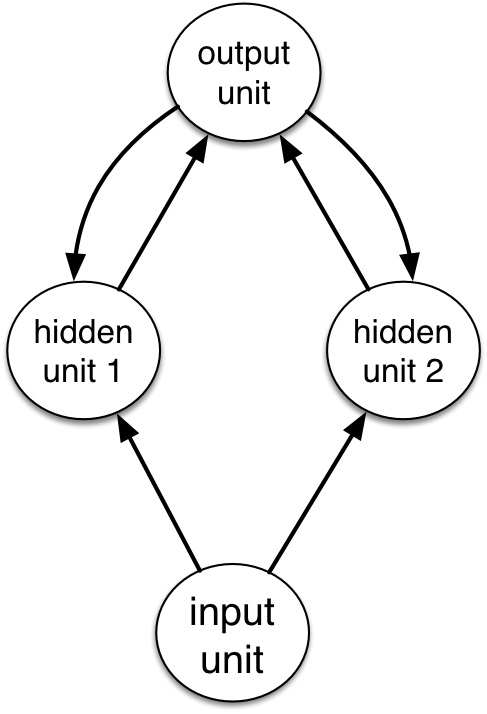
Parity Approach
Let’s find weights and biases for the RNN on the right so that it computes the parity. All hidden and output units are binary threshold units (\(h(x) = 1\) if \(x > 0\) and \(h(x) = 0\) otherise).
Strategy
- The output unit tracks the current parity, which is the XOR of the current input and previous output.
- The hidden units help us compute the XOR.
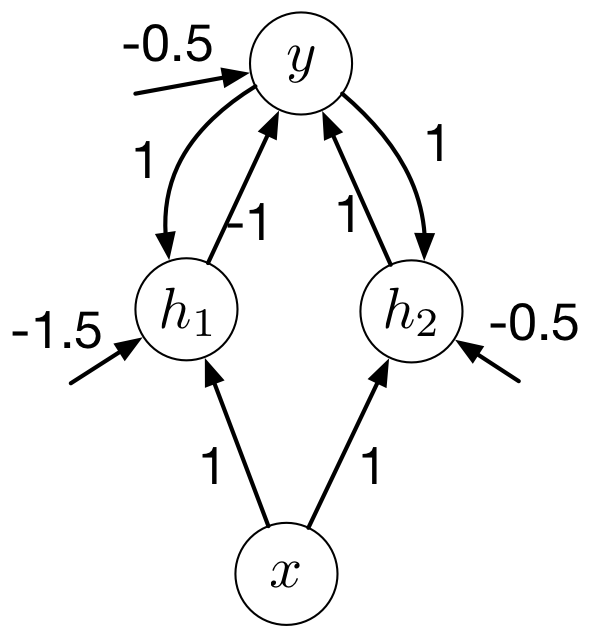
Parity Approach II
Unrolling Parity RNN
Parity Computation
The output unit should compute the XOR of the current input and previous output:
| \(y^{(t-1)}\) | \(x^{(t)}\) | \(y^{(t)}\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Computing Parity
Let’s use hidden units to help us compute XOR.
- Have one unit compute AND, and the other one compute OR.
- Then we can pick weights and biases just like we did for multilayer perceptrons.
Computing Parity II
| \(y^{(t-1)}\) | \(x^{(t)}\) | \(h_1^{(t)}\) | \(h_2^{(t)}\) | \(y^{(t)}\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Back Propagation Through Time
As you can guess, we don’t usually set RNN weights by hand. Instead, we learn them using backprop.
In particular, we do backprop on the unrolled network. This is known as backprop through time.
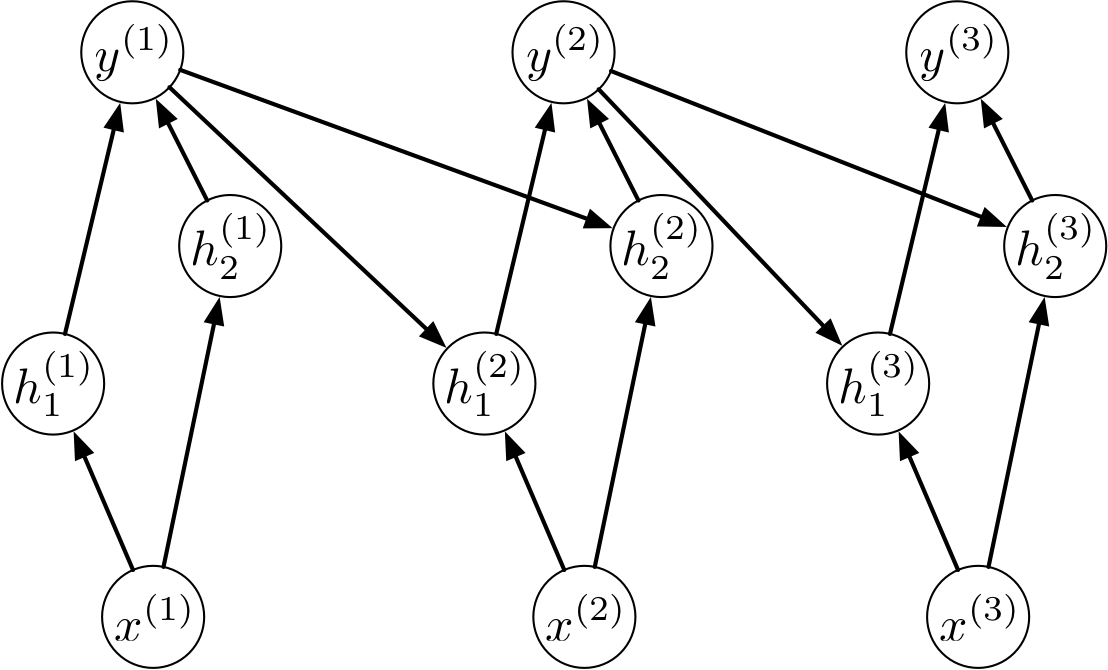
Unrolled BPTT
Here’s the unrolled computation graph. Notice the weight sharing.
What can RNNs compute?
In 2014, Google researchers built an encoder-decoder RNN that learns to execute simple Python programs, one character at a time! https://arxiv.org/abs/1410.4615

What can RNNs compute?
RNNs are good at learning complex syntactic structures: generate Algebraic Geometry LaTex source files that almost compiles:

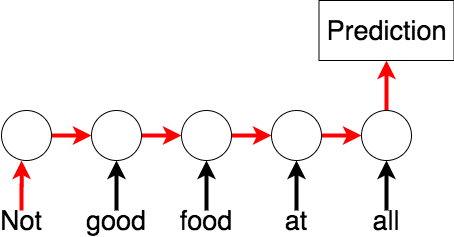
Sentiment Analysis with Recurrent Neural Networks
RNN for language modelling
Usually, the sequence of inputs \(x_t\) will be vectors. The hidden states \(h_t\) are also vectors.
For example, we might use a sequence of one-hot vectors \({\bf x}_t\) of words (or characters) to represent a sentence. (What else can we use?)
How would we use a RNN to determine (say) the sentiment conveyed by the sentence?
As usual, start with the forward pass…
RNN: Initial Hidden State
Start with an initial hidden state with a blank slate (can be a vector of all zeros, or a parameter that we train)
RNN: Update Hidden State
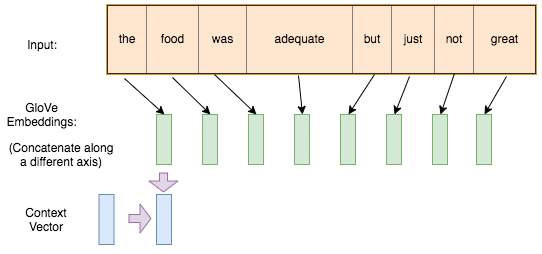
Compute the first hidden state based on the initial hidden state, and the input (the one-hot vector \({\bf x}_1\) of the first word).
RNN: Continue Updating Hidden State
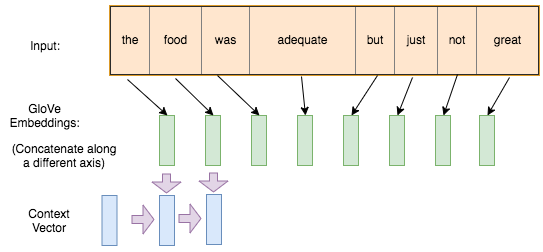
Update the hidden state based on the subsequent inputs. Note that we are using the same weights to perform the update each time.
RNN: Last Hidden State
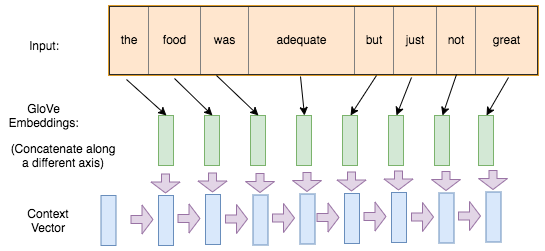
Continue updating the hidden state until we run out of words in our sentence.
RNN: Compute Prediction
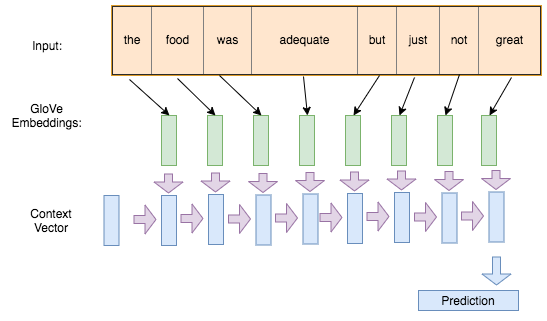
Use the last hidden state as input to a prediction network, usually a MLP.
Alternative: take the max-pool and average-pool over all computed hidden states.
Sequence Classification
Lab: let’s build this model!

Sentiment140 Data
Dataset of tweets with either a positive or negative emoticon, but with the emoticon removed.
Input: Tweet (sequence of words/characters)
Target: Positive or negative emoticon?
Example:
- Negative: “Just going to cry myself to sleep after watching Marley and Me”
- Positive: “WOOOOO! Xbox is back”
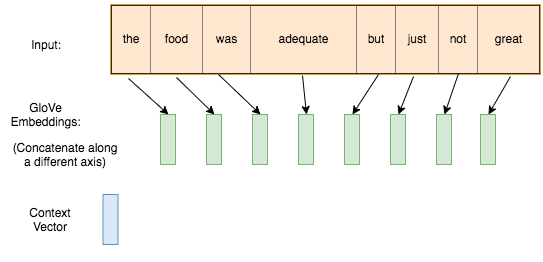
Approach

- Use GloVe embeddings to represent words as input \({\bf x}^{(t)}\) (note: we could have chosen to work at the character level)
- Use a recurrent neural network to get a combined embedding of the entire tweet
- Use a fully-connected layer to make predictions (happy vs sad)
Key Considerations
- We’ll be using the PyTorch
nn.RNNmodule, which can be unintuitive
- Batching difficulties: each tweet is a different length, so how can we batch?
- One way is to pad shorter sequences with a special “padding” token at the end of the sequence
- However, we want to minimize this padding due to computational complexity
Gradient Explosion and Vanishing
RNN Gradients
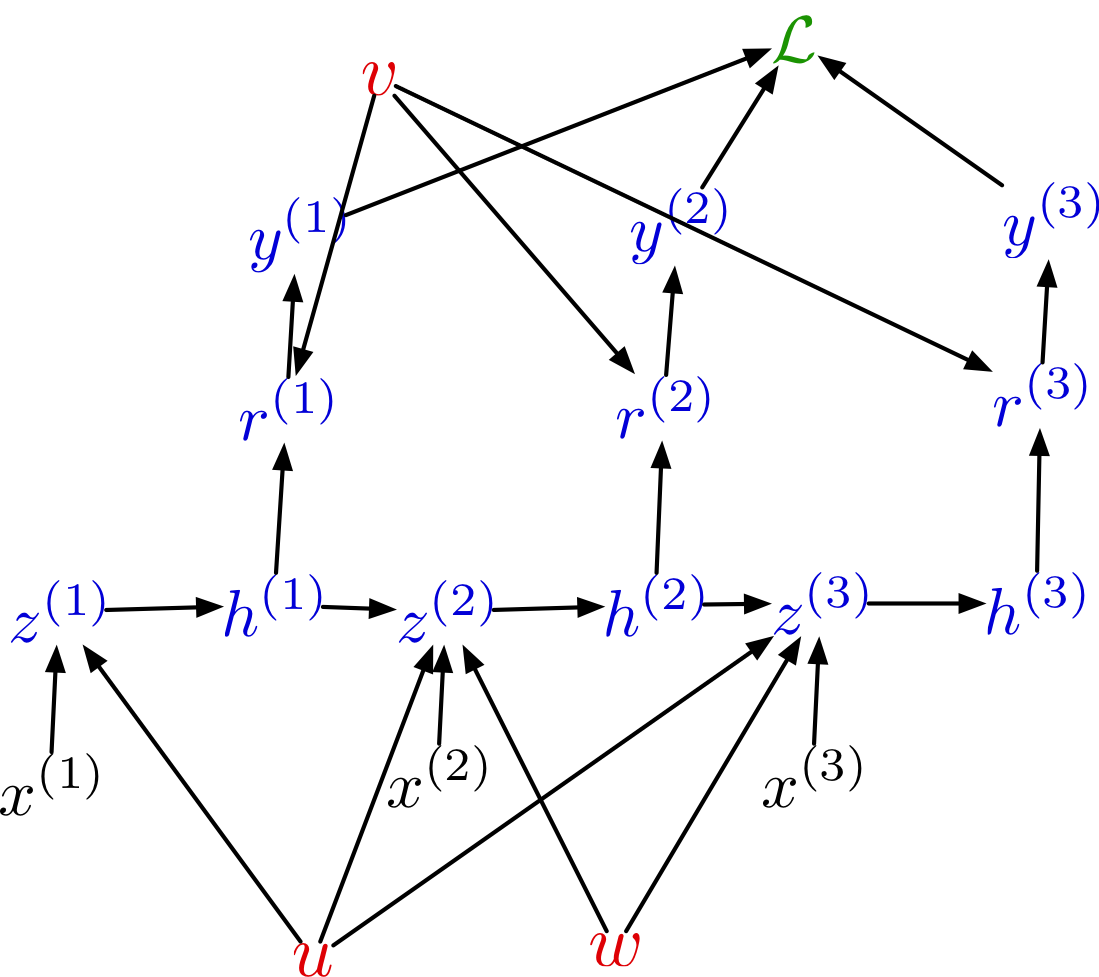
Recall the unrolled computation graph for a small RNN:

Backprop Through Time
Activations: \[\begin{align*} \overline{\mathcal{L}} &= 1 \\ \overline{y^{(t)}} &= \overline{\mathcal{L}} \, \frac{\partial \mathcal{L}}{\partial y^{(t)}} \\ \overline{r^{(t)}} &= \overline{y^{(t)}} \, \phi^\prime(r^{(t)}) \\ {\color{magenta} \overline{h^{(t)}}} & {\color{magenta}\, = \overline{r^{(t)}} \, v + \overline{z^{(t+1)}} \, w} \\ \overline{z^{(t)}} &= \overline{h^{(t)}} \, \phi^\prime(z^{(t)}) \end{align*}\]
Parameters: \[\begin{align*} {\color{magenta} \overline{u}} &{\color{magenta} \, = \sum_t \overline{z^{(t)}} \, x^{(t)}} \\ {\color{magenta} \overline{v}} &{\color{magenta} \,= \sum_t \overline{r^{(t)}} \, h^{(t)}} \\ {\color{magenta} \overline{w}} &{\color{magenta} \,= \sum_t \overline{z^{(t+1)}} \, h^{(t)}} \end{align*}\]
Key idea: multivariate chain rule!
Gradient Explosion and Vanishing
The longer your sequence, the longer gap the time step between when we see potentially important information and when we need it:
The derivatives need to travel this entire pathway.
Why Gradients Explode or Vanish
Consider a univariate version of the RNN:
Backpropagation updates: \[\begin{align*} \overline{h^{(t)}} &= \overline{z^{(t+1)}} \, w \\ \overline{z^{(t)}} &= \overline{h^{(t)}} \, \phi^\prime(z^{(t)}) \end{align*}\]
Applying this recursively: \[\begin{align*} \overline{h^{(1)}} = w^{T-1} \phi^\prime(z^{(2)}) \cdots \phi^\prime(z^{(T)}) \overline{h^{(T)}} \end{align*}\]
Why Gradients Explode or Vanish II
With linear activations: \[\frac{\partial h^{(T)}}{\partial h^{(1)}} = w^{T-1}\]
\[\textbf{Exploding:} \qquad w=1.1, T=50 \Rightarrow \frac{\partial h^{(T)}}{\partial h^{(1)}} = 117.4\]
\[\textbf{Vanishing:} \qquad w=0.9, T=50 \Rightarrow \frac{\partial h^{(T)}}{\partial h^{(1)}} = 0.00515\]
Multivariate Hidden States
More generally, in the multivariate case, the Jacobians multiply:
\[\frac{\partial {\bf h}^{(T)}}{\partial {\bf h}^{(1)}} = \prod_{t = 1}^{T - 1} \frac{\partial {\bf h}^{(t + 1)}}{\partial {\bf h}^{(t)}}\]
Matrices can “explode” or “vanish” just like scalar values, though it’s slightly harder to make precise.
Repeated Application of Functions
Another way to look at why gradients explode or vanish is that we are applying a function over and over again.
Each hidden layer computes some function of previous hidden layer and the current input: \({\bf h}^{(t)} = f({\bf h}^{(t-1)}, {\bf x}^{(t)})\)
This function gets repeatedly applied:
\[\begin{align*} {\bf h}^{(4)} &= f({\bf h}^{(3)}, {\bf x}^{(4)}) \\ &= f(f({\bf h}^{(2)}, {\bf x}^{(3)}), {\bf x}^{(4)}) \\ &= f(f(f({\bf h}^{(1)}, {\bf x}^{(2)}), {\bf x}^{(3)}), {\bf x}^{(4)}) \end{align*}\]
Iterated Functions (Intuition)
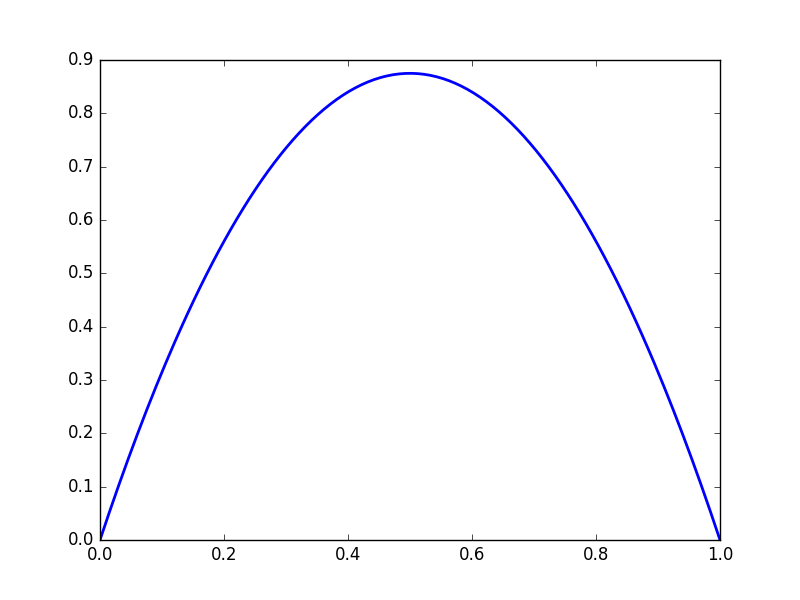
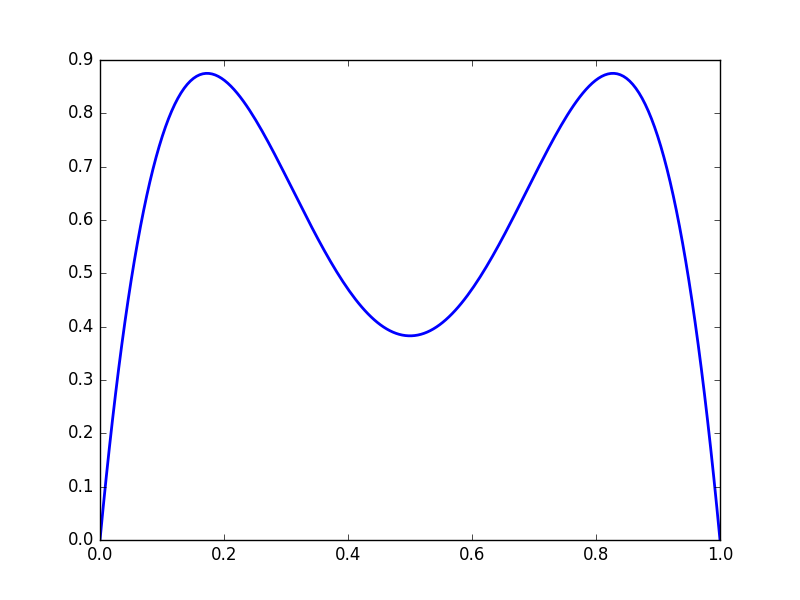
We get complicated behaviour from iterated functions. Consider \(f(x) = 3.5x(1-x)\)
\(y = f(x)\)
\(y = f(f(x))\)
\(y = f^{\circ 3}(x)\)
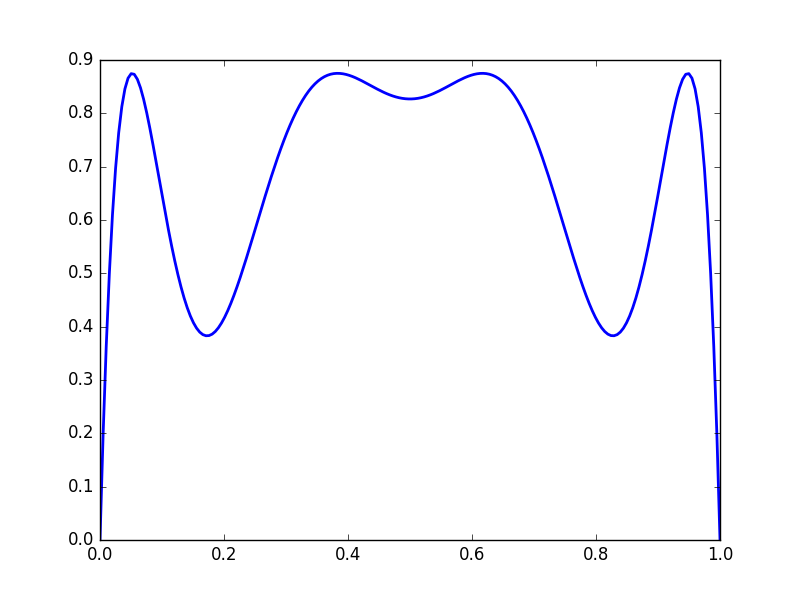
\(y = f^{\circ 6}(x)\)
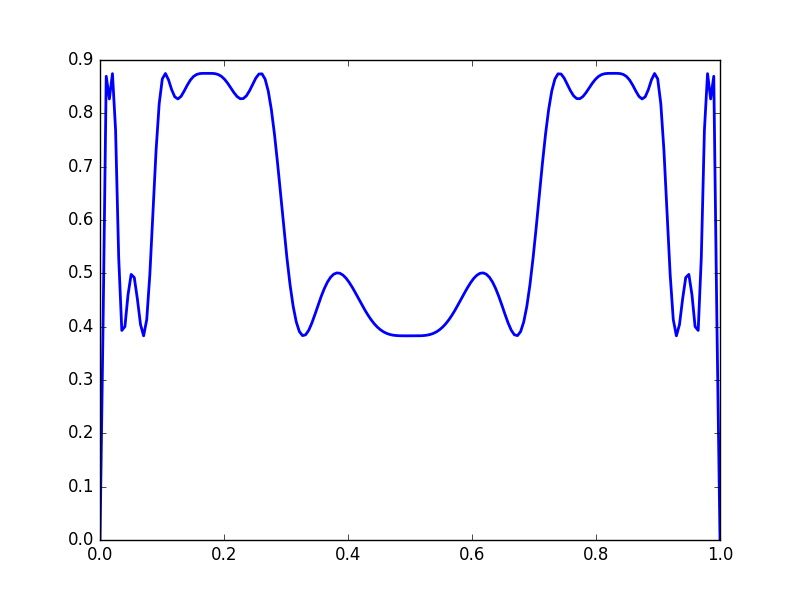
Note that the function values gravitate towards fixed points, and that the derivatives becomes either very large or very small.
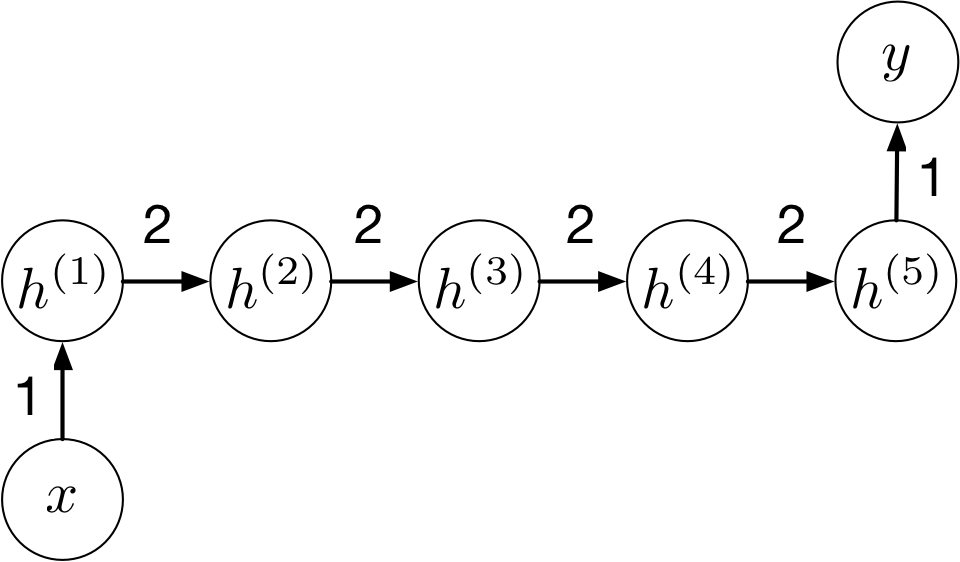
RNN with tanh activation
More concretely, consider an RNN with a tanh activation function:
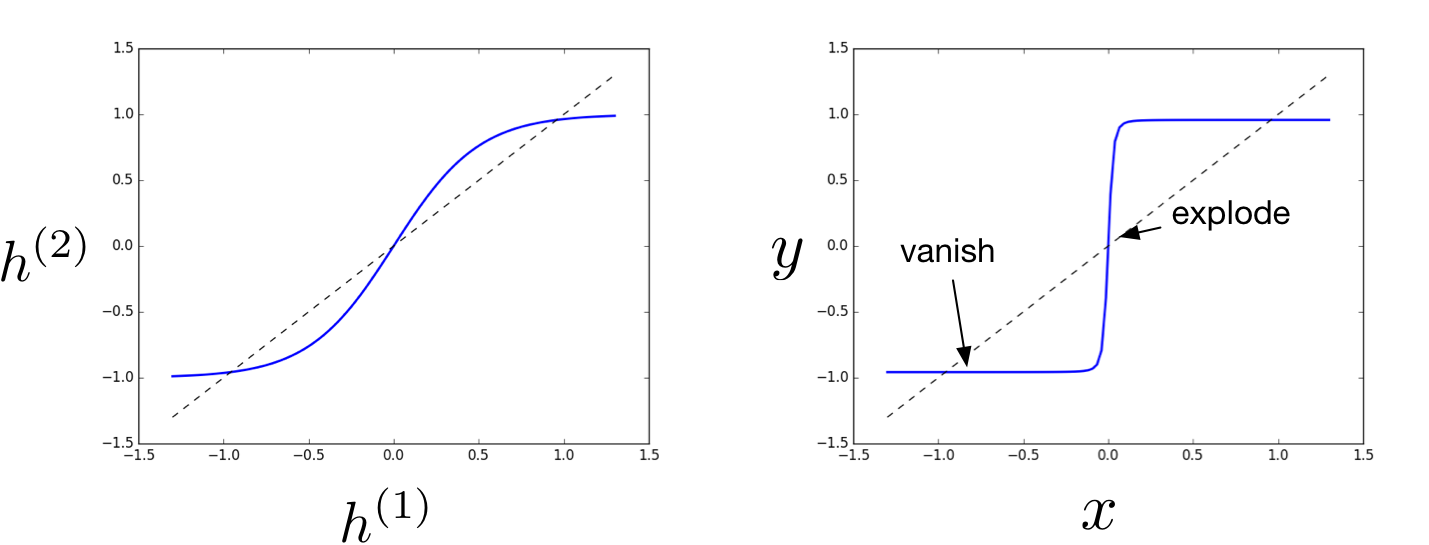
RNN with tanh activation II
The function computed by the network:
Cliffs
Repeatedly applying a function adds a new type possible loss landscape: cliffs, where the gradient of the loss with respect to a parameter is either close to 0, or very large.
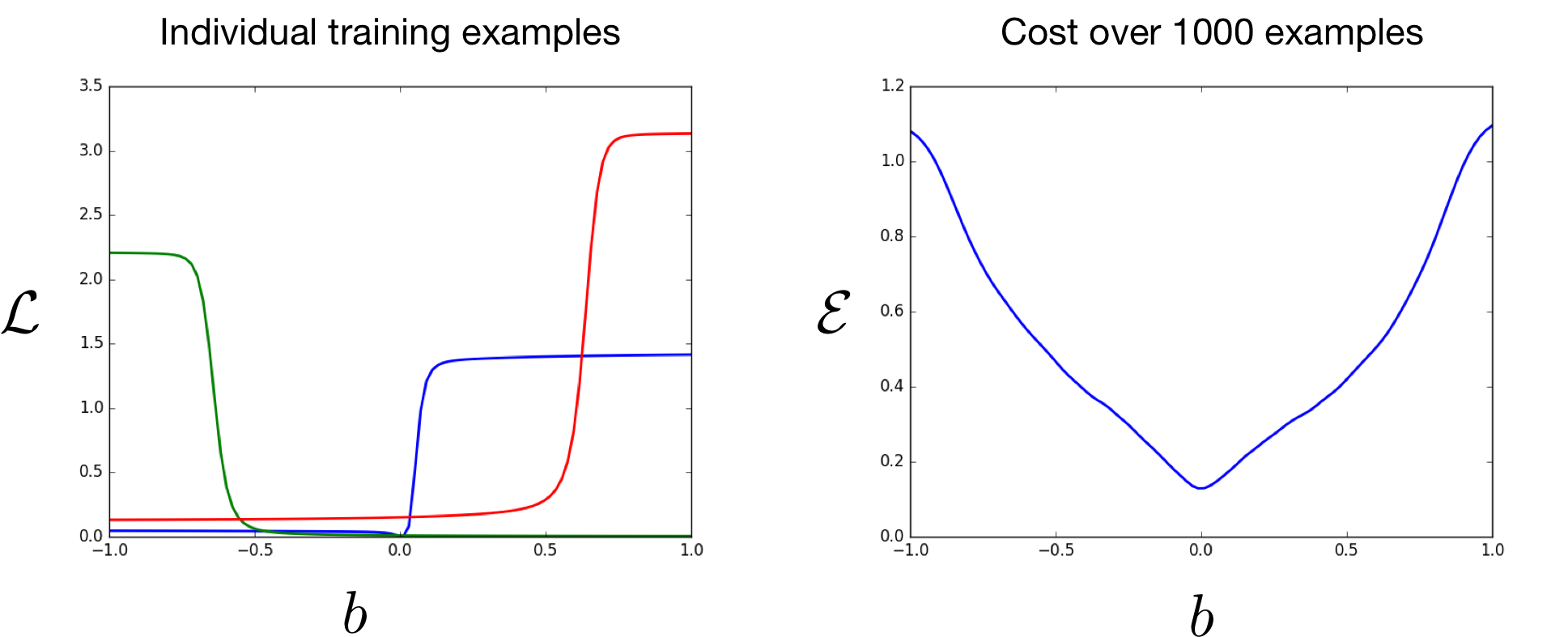
Cliffs II
Generally, the gradient will explode on some inputs and vanish on others. In expectation, the cost may be fairly smooth.
Gradient Clipping
One solution is to “clip” the gradient so that it has a norm of at most \(\eta\). Otherwise, update the gradient \({\bf g}\) with \({\bf g} \leftarrow \eta\frac{{\bf g}}{||{\bf g}||}\)
The gradients are biased, but at least they don’t blow up:
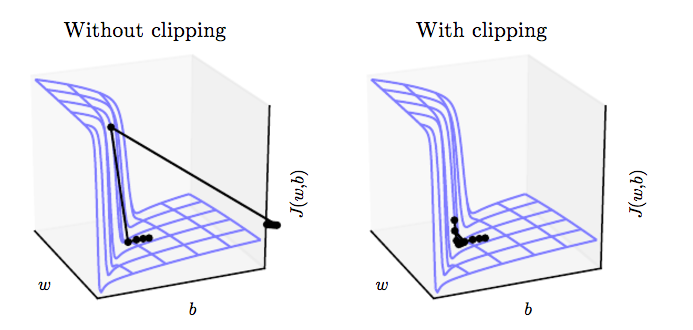
Gradient clipping solves the exploding gradient problem, but not the vanishing gradient problem.
Learning Long-Term Dependencies
Idea: Initialization
Hidden units are a kind of memory. Their default behaviour should be to keep their previous value.
If the function \({\bf h}^{(t)} = f({\bf h}^{(t-1)}, {\bf x}^{(t)})\) is close to the identity, then the gradient computations \(\displaystyle \frac{\partial {\bf h}^{(t)}}{\partial {\bf h}^{(t-1)}}\) are stable.
This initialization allows learning much longer-term dependencies than “vanilla” RNNs
Long-Term Short Term Memory
Change the architecture of the recurrent neural network by replacing each single unit in an RNN by a “memory block”:
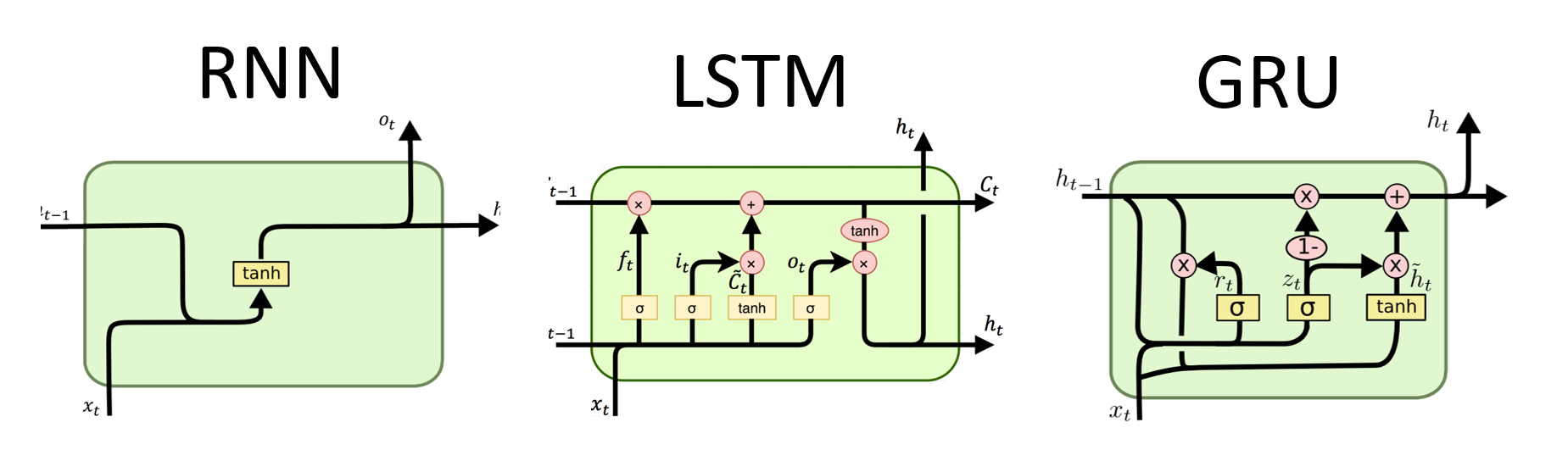
LSTM
LSTM Math
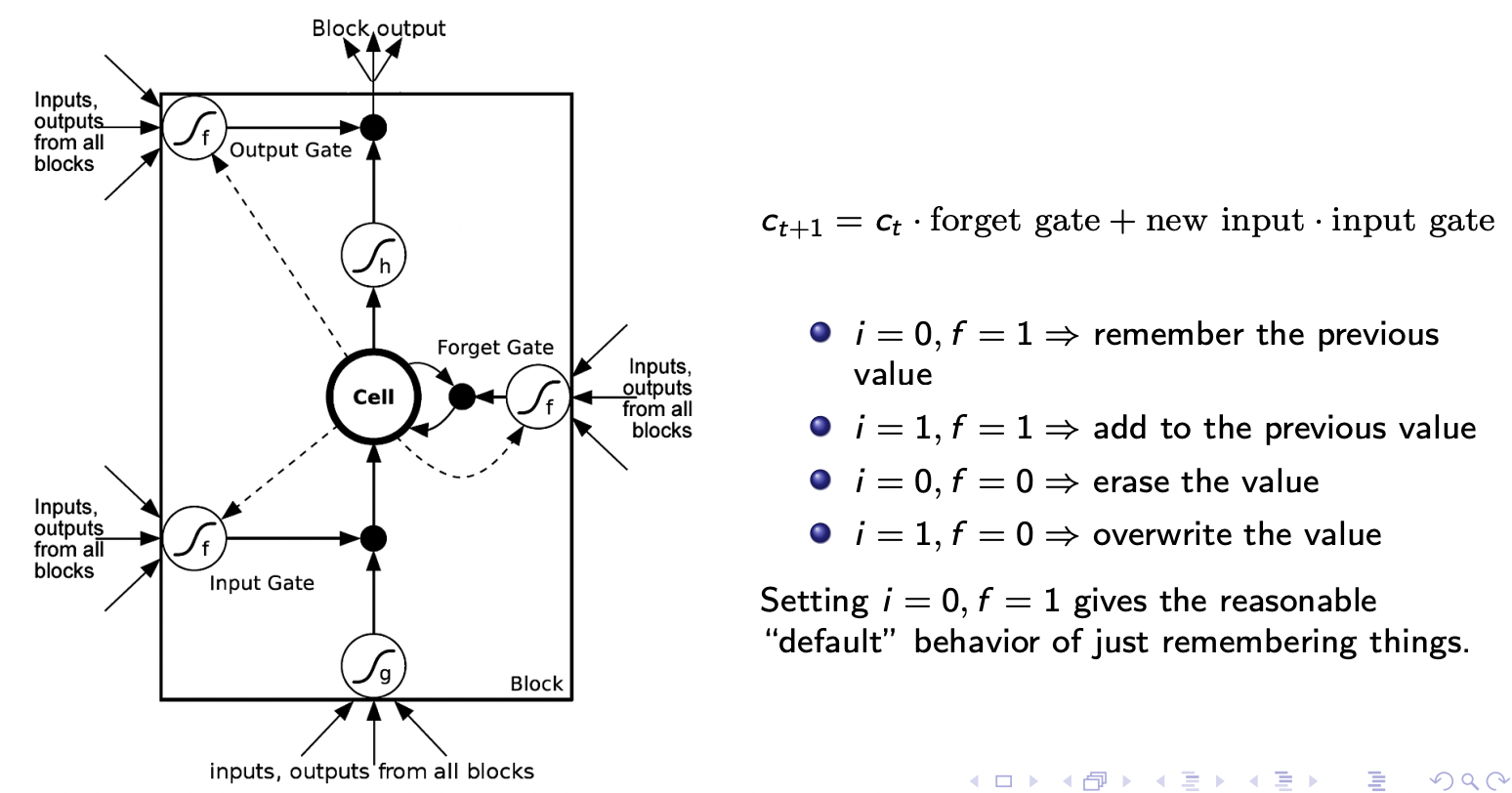
In each step, we have a vector of memory cells \({\bf c}\), a vector of hidden units \({\bf h}\) and vectors of input, output, and forget gates \({\bf i}\), \({\bf o}\), and \({\bf f}\).
There’s a full set of connections from all the inputs and hiddens to the inputs and all of the gates:
\[ \begin{pmatrix} \bf{i}_t \\ \bf{f}_t \\ \bf{o}_t \\ \bf{g}_t \\ \end{pmatrix} = \begin{pmatrix} \sigma \\ \sigma \\ \sigma \\ \tanh \end{pmatrix} {\bf W} \begin{pmatrix} {\bf x}_t \\ {\bf h}_{t - 1} \end{pmatrix} \]
LSTM Math II
\[\begin{align*} {\bf c_t } &= {\bf f_t } \circ {\bf c_{t-1} } + {\bf i_t } \circ {\bf g_t } \\ {\bf h_t } &= {\bf o_t } \circ \tanh({\bf c_t }) \end{align*}\]
Exercise: show that if \({\bf f}_{t+1} = 1\), \({\bf i}_{t+1} = 0\), and \({\bf o}_{t} = 0\), then the gradient of the memory cell gets passed through unmodified, i.e., \(\bar{{\bf c}_t} = \bar{{\bf c}_{t+1}}\).
Key Takeaways
You should be able to understand…
- why learning long-term dependencies is hard for vanilla RNNs
- why gradients vanish/explode in a vanilla RNN
- what cliffs are and how repeated application of a function generates cliffs
- what gradient clipping is and when it is useful
- the mathematics behind why gating works
Text Generation with RNN
RNN Hidden States
RNN For Prediction:
- Process tokens one at a time
- Hidden state is a representation of all the tokens read thus far
RNN For Generation:
- Generate tokens one at a time
- Hidden state is a representation of all the tokens to be generated
RNN Hidden State Updates
RNN for Prediction:
- Update hidden state with new input (token)
- Get prediction (e.g. distribution over possible labels)
RNN for Generation:
- Get prediction distribution of next token
- Generate a token from the distribution
- Update the hidden state with new token
Text Generation Diagram
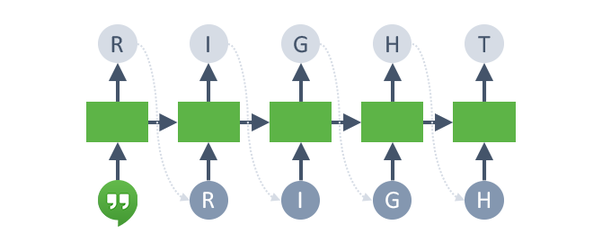
- Get prediction distribution of next token
- Generate a token from the distribution
- Update the hidden state with new token
Test Time Behaviour of Generative RNN
Unlike other models we discussed so far, the training time behaviour of Generative RNNs will be different from the test time behaviour
Test time behaviour at each time step:
- Obtain a distribution over possible next tokens
- Sample a token from that distribution
- Update the hidden state based on the sample token
Training Time Behaviour of Generative RNN
During training, we try to get the RNN to generate one particular sequence in the training set. At each time step:
- Obtain a distribution over possible next tokens
- Compare this with the actual next token
Q1: What kind of a problem is this? (regression or classification?)
Q2: What loss function should we use during training?
Text Generation: First Step

- Start with an initial hidden state
- Update the hidden state with a “<BOS>” (beginning of string) token to initiate the hidden state
- Get the distribution over the first character
- Compute the cross-entropy loss against the ground truth (R)
Text Generation with Teacher Forcing

- Update the hidden state with the ground truth token (R) regardless of the prediction from the previous step
- This technique is called teaching forcing
- Get the distribution over the second character
- Compute the cross-entropy loss against the ground truth (I)
Text Generation: Later Steps

Continue until we get to the “<EOS>” (end of string) token
Some Remaining Challenges
- Vocabularies can be very large once you include people, places, etc.
- It’s computationally difficult to predict distributions over millions of words.
- How do we deal with words we haven’t seen before?
- In some languages, it’s hard to define what should be considered a word.
Character vs Word-level
Another approach is to model text one character at a time
This solves the problem of what to do about previously unseen words.
Note that long-term memory is essential at the character level!
Sequence-to-Sequence Architecture
Neural Machine Translation
Say we want to translate, e.g. English to French sentences.
We have pairs of translated sentences to train on.
Here, both the inputs and outputs are sequences!
What can we do?
Sequence-to-sequence architecture
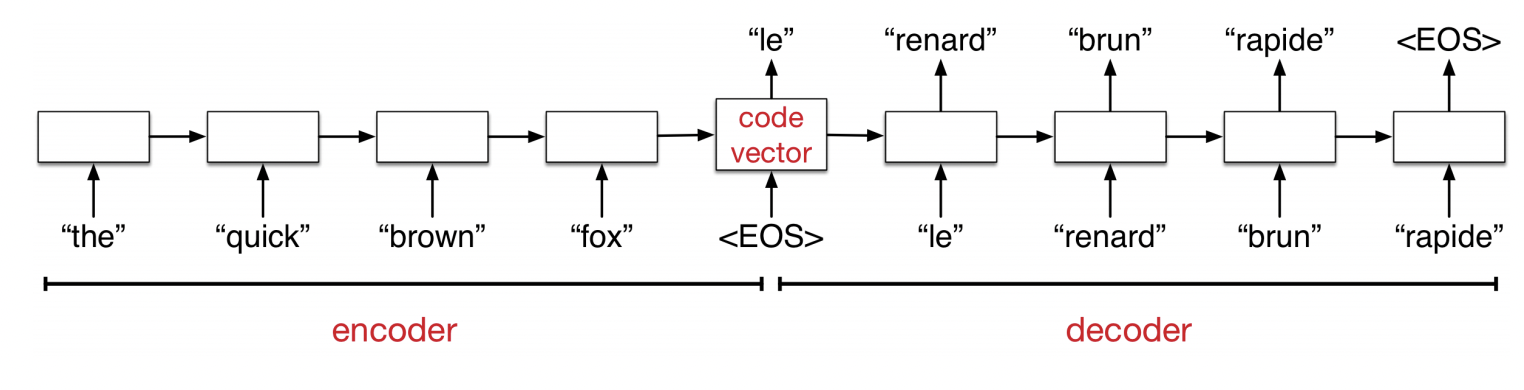
The network first reads and memorizes the sentences.
When it sees the “end token”, it starts outputting the translation.
The “encoder” and “decoder” are two different networks with different weights.
Wrap Up
Summary
- Recurrent Neural Networks can be used for learning sequence data
- Training RNNs may suffer from gradient explosion and vanishing
- Important Applications of RNNs are text generation and sequence to sequence modelling